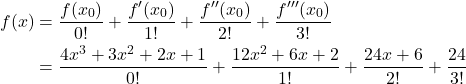Taylor'sche Entwicklung - Maximilian R. Schlechtinger

Taylor’sche Entwicklung

Taylor-Entwicklung

Der Vollständigkeit halber nochmal die Herleitung der Taylor’schen Formel, so wie sie in der Vorlesung Analysis 1 geschehen ist. Die Formel von Taylor besagt grundsätzlich, dass sich eine Funktion über einen Term bestehend aus ihren Ableitungen beschreiben lässt. Wir gehen dabei davon aus, dass wir es mit einer Funktion vom Grad $n$ zu tun haben und auch, dass die $n-te$ Ableitung existiert.
Die Herleitung orientiert sich dabei an vorhandenem Wissen über den Mittelwertsatz.

Mittelwertsatz XXL

Zu einer gegeben Funktion $f(x)$ in einem gegebenen Intervall $[x;x_0]$ gibt es einen Wert $\xi$ mit $f(\xi)$
Wir formen den den Term der Funktion wie folgt um:

$\begin{align*}f(x) &= f(x_0) + f'(\xi) \cdot (x-x_0) \\&= f(x_0) + f'(x_m)(x-x_0) + \left(f'(\xi)-f'(x_m)\right)(x-x_0)\end{align*}$

Übergang zur Taylor-Entwicklung

Die Entwicklung nach Taylor, einer Funktion an der Stelle $x$ folgt folgender Regel

$\begin{align*}f(x)=f(x_0)+f'(x_0)(x-x_0)+f''(\xi)\frac{(x-x_0)^2}{2!}\end{align*}$

Daraus ergibt sich eine allgemeine Form:

$\begin{align*}f(x)=\left(\sum_{j=0}^{n} f^{(j)} (x_0) \cdot \frac{(x-x_0)^j}{j!} \right) + f^{n+1} (\xi) \frac{(x-x_0)^{n+1}}{(n+1)!}\end{align*}$

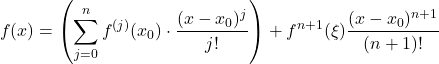
Wir wählen als einfaches Beispiel die Entwicklung des Polynoms $f(x)=4x^3+3x^2+2x+1$ . Die Ableitungen erhalten wir durch einfaches Anwenden der bekannten Ableitungsregeln

$\begin{align*}f(x)= 4x^3+3x^2+2x+1 \\f'(x)= 12x^2+6x+2\\f''(x)= 24x+6\\f'''(x)= 24\\\end{align*}$

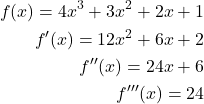
Gemäß der Taylor-Entwicklung im Punkt $x_0$ erhalten wir die nachfolgende Form. Der Vollständigkeit halber sind alle Brüche mitbedacht, um die Kohärenz der Fakultäten zu zeigen.

$\begin{align*}f(x) &= \frac{f(x_0)}{0!} + \frac{f'(x_0)}{1!} + \frac{f''(x_0)}{2!} + \frac{f'''(x_0)}{3!} \\&= \frac{4x^3+3x^2+2x+1}{0!} + \frac{12x^2+6x+2}{1!} + \frac{24x+6}{2!} + \frac{24}{3!}\end{align*}$

Maximilian R. Schlechtinger

Taylor’sche Entwicklung

Taylor-Entwicklung

Mittelwertsatz XXL

Übergang zur Taylor-Entwicklung

Inhalt

You don't meet people by accident