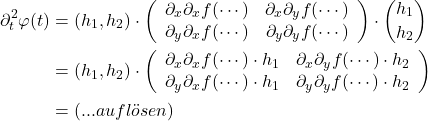Gradient einer Funktion

Ein Gradient ist so etwas wie die Ableitung einer Funktion aus dem $\mathbb{R}^n$ . Vom Gedanken her läuft man bei dieser Art der Ableitung die Funktion einmal in x-Richtung und einmal in y-Richtung ab. Vieles davon ist im Grunde Matrix-Multiplikation, daher der Vektor mit den beiden Ableitungen. Als Erinnerung, die Ableitung funktioniert quasi nach der Kettenregel $F(g(t))\frac{d}{dt}=F'(g(t)*g'(t)$ . Das * bezeichnet das \textit{Skalarprodukt}.

$\begin{align*} \varphi(t) &= F\left(g(t), f(t)\right) \\ \varphi'(t) &= \nabla F\left(g(t),f(t)\right) * \binom{g'(t)}{f'(t)} = \left(\partial_x F, \partial_y F \right) \cdot \binom{g'(t)}{f'(t)} \end{align*}$

\section*{Analyse von $f(x,y)$ auf Geraden $G$ }

$\begin{align*} F(x,y): \mathbb{R}^2 \rightarrow \mathbb{R} \end{align*}$

Wir betrachten ab jetzt die Ableitung \textit{entlang von Kurven}. Diese Kurven sind praktischerweise Geraden und wir bezeichnen sie mit $G$ . Wobei $h_1 , h_2 \in \mathbb{R}$ , beliebig, aber fest.

$\begin{align*} G: \binom{x}{y} =\binom{th_1}{th_2} \end{align*}$

Es ist quasi der Versuch, die Umgebung von $(0,0$ zu untersuchen. Wir kennen aus 1D (Taylor).

$\begin{align*} \varphi(th)=\phi(0)+\varphi'(0)\cdot h + \frac{1}{2} \varphi''(\xi)*h^2 \end{align*}$

\section*{Taylor-Entwicklung in 2D}
Wie wir später sehen werden ist die 1D-Taylor-Entwicklung lediglich ein spezialfall der allgemeineren Form. Da die Herleitung allerdings in über Funktionen $\mathbb{R}^1 \rightarrow \mathbb{R}^1$ geschehen ist, ist das nicht aufgefallen. Wir verallgemeinern nun.

$\begin{align*} \varphi' : (bekannt) \\ \notag \\ \varphi'' = \partial_t \varphi(t) = \partial_t f(th_1 , th_2) = \nabla f(th_1 , th_2) * \binom{h_1}{h_2} \\ \end{align*}$

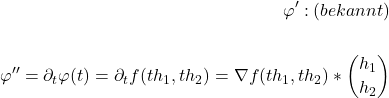
Wir bilden nun die zweite Ableitung in höheren Dimensionen. Anstelle einer einzelnen Zeile (wie etwa in 1D) erhalten wir eine Matrix mit den jeweiligen partiellen Ableitungen.

$\begin{align*} \partial_t^2 \varphi(t) &= \partial_t \left\{\partial_x f(th_1,th_2) \cdot h_1 + \partial_y f(th_1,th_2) \cdot h_2 \right\}\\ &= \left\{\partial_t \cdot \partial_x f(th_1,th_2) \cdot h_1 + \partial_t \cdot \partial_y f(th_1,th_2) \cdot h_2 \right\}\\ &= \nabla (\partial_x f(th_1,th_2) \cdot h_1) \binom{h_1}{h_2} + \nabla (\partial_y f(th_1,th_2) \cdot h_2) \binom{h_1}{h_2} \\ &= \left(\partial_x \partial_x f(th_1,th_2) \cdot h_1 , \partial_y \partial_x f(th_1,th_2) \cdot h_1 \right) \binom{h_1}{h_2} \\ &+ \nabla \partial_y f(th_1,th_2) \cdot h_2 \binom{h_1}{h_2} \\ &=\left(\partial_x \partial_x f(\cdots)h_1 \right) \cdot h_1 + \left(\partial_y \partial_x f(\cdots)h_1 \right) \cdot h_2 \\ &+ \nabla \partial_y f(\cdots) \cdot h_2 \cdot \binom{h_1}{h_2} \end{align*}$

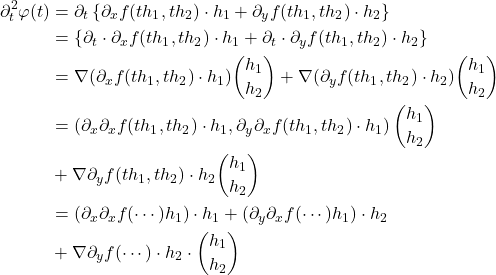
Wir sammeln dann alle Terme ein und schreiben die Gradienten als Matrix:

$\begin{align*} \partial_t^2 \varphi(t) &= (h_1, h_2) \cdot \left( \begin{array}{cc} \partial_x \partial_x f(\cdots) & \partial_x \partial_y f(\cdots) \\ \partial_y \partial_x f(\cdots) & \partial_y \partial_y f(\cdots) \\ \end{array} \right) \cdot \binom{h_1}{h_2} \\ &= (h_1, h_2) \cdot \left( \begin{array}{cc} \partial_x \partial_x f(\cdots) \cdot h_1 & \partial_x \partial_y f(\cdots) \cdot h_2 \\ \partial_y \partial_x f(\cdots) \cdot h_1 & \partial_y \partial_y f(\cdots) \cdot h_2 \\ \end{array} \right) \\ &= (... auflösen) \end{align*}$

Maximilian R. Schlechtinger

Gradient einer Funktion

Inhalt

You don't meet people by accident